Get Into The Swing
By Tony Bee (a.k.a. ‘Tony’ on the Low Limit Poker Forum).
Here’s a quick arithmetic test. (Don’t groan, it’s for your own good.)
Fill in the answer: 1 + 4 x 2 = ?
Quick as you can, no calculators allowed. Got it?
(I’ll tell you the answer at the end of this article, but here’s a clue: the answer is not 10.)
Numbers. To some they’re a source of fascination, to others a source of frustration and confusion.
As a poker player you may have hoped that arithmetic and statistical considerations could be left back in the classroom, apart from perhaps whether you have the pot odds to call with your gutshot on a rainbow flop. And let’s face it, you can simply memorize a chart to work that out.
But you’d be wrong. If you’re serious about the game there is one particular, very special number that you would do well to be on close terms with.
However, only a fraction of poker players have heard of it, an even smaller fraction know how to calculate it and I’d be willing to wager that only a teeny tiny percentage know what to do with it. Yet it’s one of the most important and useful numbers a poker player (or indeed any advantage gambler) needs to know. What is it?
Two words: STANDARD DEVIATION.
In this article I shall endeavour to explain what the big deal is about standard deviation (from here on I’ll call it SD), and I’ll give examples of how it can be used to help and inform your game. Don’t worry if you’re not a ‘numbers person’. There will be some arithmetic, but I’ll try to keep it light. If you have any questions you can always contact me at the forum.
How is Standard Deviation (SD) Calculated?
If you play online, the simplest way to find your SD is to purchase one of a number of software packages designed to do this for you. I personally use Poker Tracker, but there are a number of software packages with this capability. Poker Tracker is able to automatically import your hand histories as you play and update your statistics (and those of your opponents) in close to real time.
However, if you only play live or you’re too tight to buy one of these packages, you’ll need to know how to calculate this yourself.
Here’s an example.
Let’s suppose you play 5/10 limit, and you want to calculate your SD. You firstly have to decide what unit of measurement you wish to use. Some people prefer to calculate their SD per hour; others prefer to use SD per 100 hands.
In fact you can use any unit you like, but most online players quote their SD in big bets per 100 hands (bb/100), and this is my personal preference. Let’s suppose that your last five sessions have gone as follows:
| Session | Result (in $) | Hands played |
| 1 | 300 | 300 |
| 2 | 450 | 800 |
| 3 | -350 | 200 |
| 4 | 150 | 300 |
| 5 | -250 | 400 |
All of the major poker sites will provide you with the number of hands played at the click of a button. All you have to do is make a note of this along with your net win (or loss) at the end of each session.
It is also convenient to convert your session results as follows:
| Session | Result (in big bets) | Hands played/100 |
| 1 | 30 | 3 |
| 2 | 45 | 8 |
| 3 | -35 | 2 |
| 4 | 15 | 3 |
| 5 | -25 | 4 |
| Total | 30 | 20 |
All I’ve done here is to firstly divide each number in the ‘Result’ column by the big bet (by 10 in this example), and secondly I’ve divided the ‘Hands played’ column by 100 since we want to calculate the SD in bb/100. (Note that if you were calculating your SD in hours, this second step would not be necessary.)
To estimate your SD you must use the blue numbers in each column to calculate the following (which I’ve called ‘ R ’):
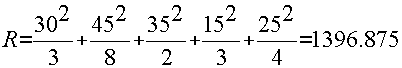
(You should be able to see where I’ve got the numbers from just by looking at the table. It’s quicker than me trying to explain it.)
You also need to calculate your mean (or ‘average’) result per 100 hands (which I’ve called ‘ M ’) using the red numbers in the table:
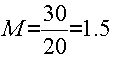
Then use the following formula to find your VARIANCE (which I’ve called ‘ V ’):
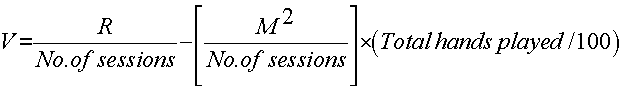
So in our example, this comes to:
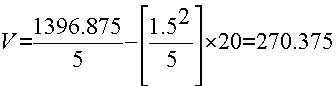
Your SD is simply the positive square-root of the variance, so:
![]() big bets per hundred (1 decimal place).
big bets per hundred (1 decimal place).
This is tedious to calculate by hand, but takes a matter of seconds if you use a spreadsheet.
It is important to note that five sessions is much too few to make a decent estimate, and you should really wait until you have around 30 sessions or more. Even then your M and SD are only estimates. The more sessions you have under your belt, the better.
Now, having gone to the trouble of calculating our SD, let’s look at some examples of what we can do with it.
What is Standard Deviation and Why is it Useful?
Let’s suppose that your win rate per 100 hands is 1 big bet. Many players reckon therefore that if they play say, 1000 hands they should expect to be ahead by about 10 big bets. Is this true? Certainly not.
In any gambling game, if you consistently make decisions with a positive expected value, you will turn a profit in the long run. IN THE LONG RUN. But in the short term, your actual results will VARY. The extent of this variability can be measure in terms of your SD.
The SD provides a measure of how much your observed results vary from your mean (or average) result.
In plain English, your SD can give you information about the nature of your play and provide insights into how to manage your bankroll. It provides a way of measuring how ‘wild’ your session-to-session swings are.
A small SD tends to indicate a conservative, consistent player who doesn’t take undue risks. A large SD tends to indicate just the opposite. Players who have a very large SD will experience very large swings in their bankroll. Passive games also tend to lead to a smaller SD, whereas very wild games tend to lead to a larger SD. (Of course they may also lead to more profitable games, but that’s another article.)
For all practical purposes it turns out that around 98% of the time your results will lie within 3 standard deviations of your mean (average) win.
Using the results we calculated above our current win rate was 1.5 bb/100 and our SD was about 16 bb/100. So 3 SDs above our average result is 49.5 bb/100 and 3 SDs below is -46.5.5 bb/100. This means that if you play 100 hands, then 98% of the time you are as likely to be DOWN 46.5 big bets as you are UP 49.5 big bets. Remember, this is if you are a WINNING player to the tune of 1.5 bb/100!
But what if you play double this many hands (that is, 200 hands)? Does the SD then double? Well in fact, no it doesn’t. Although the amount you will win in a given period of time will theoretically double (on average), your SD will in fact NOT double. You multiply your SD by the square root of two. So in this case your SD is only approximately 23 bb/100 (which is 16 multiplied by the square root of 2).
This means that after 200 hands you are as likely to be DOWN 36 big bets as you are to be UP 100 big bets (I’ll let you work it out).
After 300 hands your average win (per hour) will triple, but your SD will be multiplied by the square root of 3, and so on.
Swings are all part of the game. They are not a problem, and neither are they something you can avoid. As long as you continue to make better decisions that your opponents, you HAVE to profit in the long run.
But hopefully you can see that the SD is useful in helping us to understand (and come to terms with) the swings in the game. This leads us naturally to…
Bankroll Management
If you play with a bankroll that is too small, the probability of you going broke (called ‘risk of ruin’ or ROR) is much greater than it would be if you have an adequate bankroll. This is fairly obvious, yet many people are blissfully unaware that they are playing way above their financial limits (until it’s too late).
To estimate the size of bankroll you need you can use this formula:
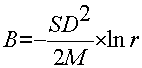 ,
,
where ‘SD’ and ‘M’ are as defined earlier, and ‘r’ is the risk of ruin you are willing to accept. The ‘ln’ on the right hand side of the formula is the ‘natural log’ function (or log to the base e) which can be found on any scientific calculator or spreadsheet. If you’re not mathematically inclined don’t worry about it, just borrow your little sister’s calculator and use it.
Only you can decide what level of risk you are willing to accept. The more ‘risk averse’ you are, the smaller your ‘r’ should be.
(This formula assumes that you will play forever at the same limit or go broke. If you are willing to drop a limit if things start to go wrong then the required bankroll can be significantly reduced.)
Most people are willing to live with a 5% ROR (use 0.05 for ‘r’ in the formula), but you may feel more comfortable with a 1% ROR (use 0.01 for ‘r’ in the formula). The smaller your ROR, the larger the bankroll you will require.
In the example above, our SD was around 16 bb/100. If we are happy to accept a 5% ROR, then the bankroll required would be estimated as follows:
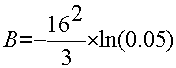 ,
,
which is approximately 256 big bets.
However, if the thought of losing your bankroll 1 time in 20 is more than you could bear, then you may want to use a 1% ROR. In this case your bankroll would need to be approximately 393 big bets. You pays your money, you takes your choice.
You may prefer to use this formula slightly differently and express the ROR in terms of the bankroll, as shown below:
![]()
where ‘ e ’ is the exponential function (use your sister’s calculator again).
This can be used to estimate your ROR given a fixed bankroll. For example, let’s say you have $1500 in your bankroll and you want to know if 150 big bets are enough to play 5/10. Your M is 1.5 and your SD is 16, as given above. What is your risk of ruin?
Substituting the appropriate values into this formula gives:
![]() , or around 17%.
, or around 17%.
So if you’re willing to live with going broke 17% of the time, go ahead and play. If not, play at a lower limit until you have a large enough bankroll to reduce your risk. Whatever you do, do not play with ‘scared money’.
Remember that these values assume that your SD and win rate are reasonably accurate, which they may not be when you first start playing. In this case I’d recommend that you always have at least 300 big bets in your bankroll until you can have more confidence in your statistics.
Summary
Hopefully this article has persuaded you of the value of tracking your standard deviation, and has given you some idea of what it’s all about. I’ll explore the statistical aspects of the game in more detail another time, but for now just remember these three things:
- Don’t expect to win every session. You won’t, and provided you are a winning player that’s nothing to worry about.
- Don’t chase the money to try and recoup your losses unless you are a favourite in the game.
- Make sure you have a bankroll that is large enough to see you through the swings, and a risk of ruin that enables you to sleep soundly at night.
Finally, I said I’d give you the answer to the arithmetic test in the first paragraph. Did you get it right? The answer is 9, not 10, because in the absence of other information we should always multiply before we add.
If you got this correct, go to the top of the class. If you didn’t, don’t worry. Just borrow your sister’s calculator next time.

